Anthony Higney

Post-doc Economist

5 minute read

Imagine a study finds labeling paid family leave as “supported by the Republican Party” increases support by 10 percentage points. What would be the effect if the issue were climate policy? Or if the cue were that Democrats support it? What about in an entirely different country? In short, how much does one estimate tell us about future estimates? In two papers Clifford, Leeper and Rainey examine how much we can infer about the general population of estimates using a single estimate.

  1. Generalizing Survey Experiments via Topic Sampling.

  2. Limits of Single‑Topic Experiments.

Finding why estimates differ

The first paper is effectively a study with a large number of treatment arms. Their choice of treatment in all arms is partisan cue. Partisan cue is where a policy is tied to a political party, and people are asked about support for that policy, and each arm has a different policy (or topic). Now this is the interesting part, they use partisan cue because it is noted as having high variation in the treatment effect estimates. They can therefore investigate why treatment effects vary. But what’s particularly interesting is how they do this.

They say an individual study of partisan cue might not give much information on what a new estimate of partisan cue is. A meta-analysis of partisan cue studies could give the average of the treatment effects, but may suffer from publication and selection bias, leading to distorted estimates of the average of treatment effects across all possible topics (e.g. researchers may choose particular policies they know will have more of a partisan cue effect). They propose an alternative to standard meta-analysis: random topic selection.

A topic here is the policy or message being used in the partisan cue experiment, such as support for foreign aid or drug legalisation. In principle though, any characteristic of a population of treatments could be used. Why is this interesting? In principle, random sampling of treatment effects to investigate could give an unbiased estimate of the average of the population of such treatments. If you have different sub-groups of treatments (e.g. in their paper economic vs social issues) you can investigate why effects are different and get conditional averages.

Now, I’ll get into the issues with this later but here’s what they find:

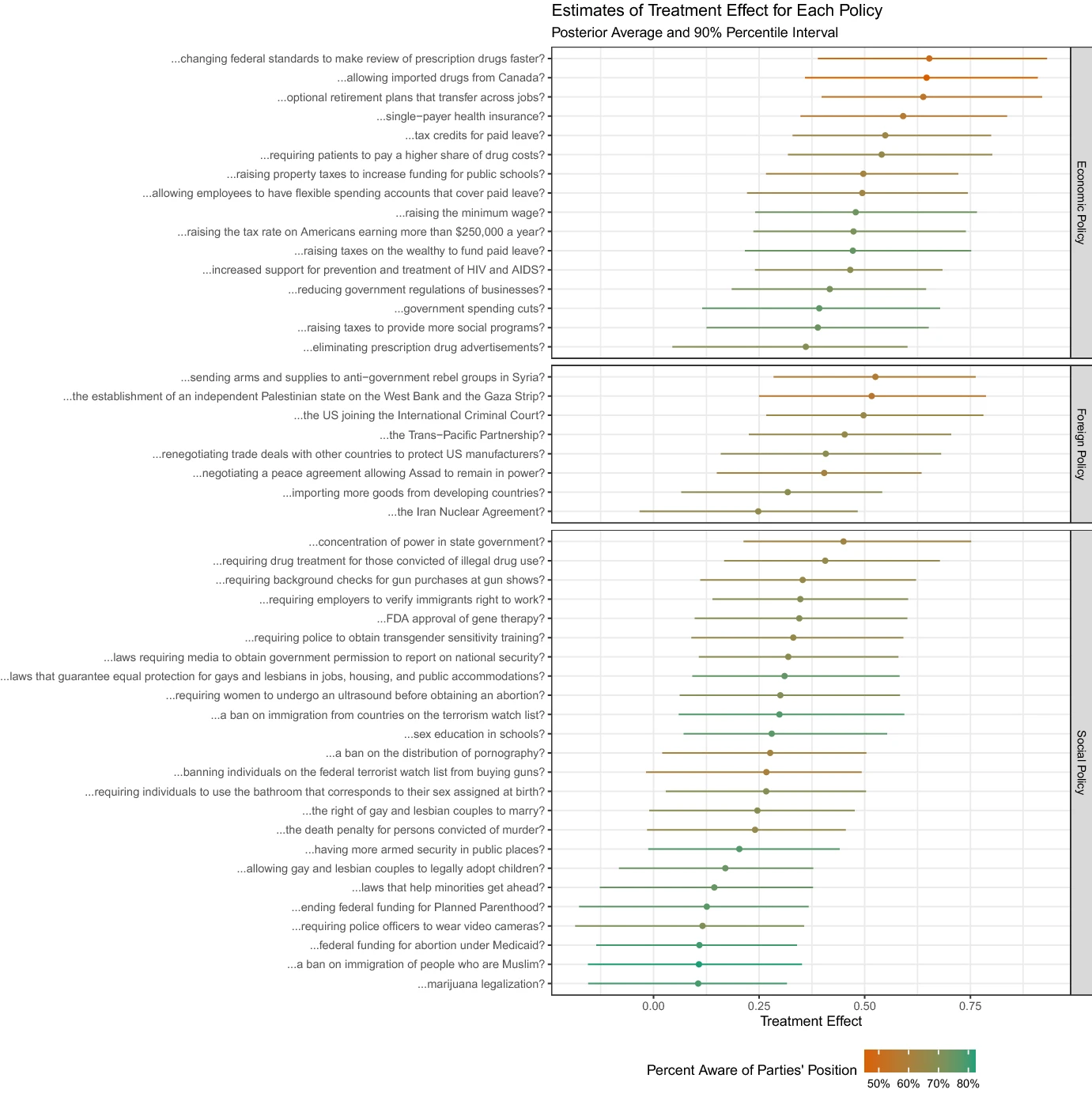
Figure 1 from Clifford, Leeper & Rainey 2024. Quote: "Figure shows the estimates of the treatment effects for each policy. The policy stems are separated into the three policy categories and ordered within each category from the largest estimate (top) to the smallest estimate (bottom). The color indicates the percent aware of the parties’ positions on the issues. Green points and lines indicate high awareness and orange points and lines indicate low awareness. While partisan cues have generally positive effects, the magnitude of the effect varies substantially across issues". I would also say economic issues tend to have larger partisan cue effects than social issues.

Basically, there is a lot of variation in partisan cue effects by topic, but treatment effects are positive. Economic partisan cue effects tend to be larger than social issues (the hypothesis being these are more difficult issues to form an opinion on so the “partisan cue” provides more of a signalling effect). They also find that topics people know more about have less of a partisan cue effect. In effect, a big reason partisan cue estimates differ is due to the person’s knowledge about the issue, and how simple it is to know what the partisan status already is. The partisan cue is a signal, and how informative that signal is depends on what new information it adds.

Criticism

Now I do find this interesting, but, of course, there are issues. Firstly, how does one determine the population of treatment effects to be sampled from, and therefore the sampling frame? The authors acknowledge this is an issue. They use a database of all questions asked by pollsters in 2016, but then how is that so different from doing a meta-analysis of previous studies? In both cases, you are basing it on what has been done rather than what could have been done.

One answer to this is that it is the same authors in the same setting doing each topic. Therefore, it is a more controlled environment to see the effect of an estimate characteristic, such as topic, when all else is equal. Unfortunately, topic is only one variable that may differ between estimates. Other things like data cleaning, researcher effects, implementer effects, etc, can differ. For example, if you clean your data one way and someone else does it another way, you will get different estimates. How do we know your estimate is closer to what a new study would find than theirs? In fact, this was found to be the main reason researchers found different effects even when using the same data. One example of the data cleaning here is that a research assistant classified the topics into topic categories. A different classification could have produced different results. It’s plausible that averaging across many researchers, where the noise of such decisions is taken into account in the estimate, could provide a better prediction. In that case is a single multi-topic study really better than a meta-analysis?

Is a single estimate anywhere near the average of estimates?

In their second paper, they build on the results of the first. They ask, for any single topic (remember whole papers are written using only one topic), how likely is it the confidence interval covers the average of the sample effect sizes. They call this an estimate of the generalizability or external validity of the estimate. I take that to mean the average of the effect sizes is a good predictor of future treatments, so the interval covering the average is better than not.

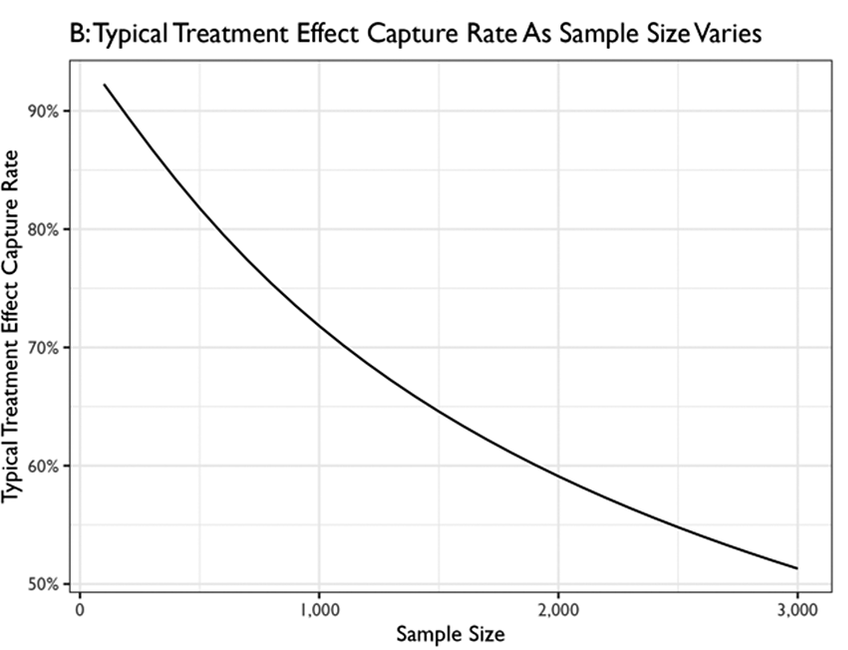
To measure whether an interval covers the average, they use simulations, but those simulations use the sampling error, and the between-topic heterogeneity from the many-topic study (you might recognise these as standard components needed for a random effects meta-analysis). For simulations of N=1000 and using these variances, they find that 28% of intervals do not cover the average of the estimates. Their take-away: any single study confidence interval could be a poor estimate of a new effect size.

They also point out that the more precise an estimate, the less likely its interval covers the average. This is purely mechanical: lower sample, less precise studies have wider intervals. Nevertheless, if the underlying effect size population has a high variance, a precise estimate interval could still be very far from what a new effect size will be, and remember this is just varying studies by topic. There are innumerable ways estimates might be different from each other. So the chance of any single study giving a good idea of the magnitude of a new estimate may be miniscule.

Figure 1 from Clifford, & Rainey 2025. Quote: " This figure shows how well the CI from a single-topic study captures the typical treatment effect in a larger population of possible experiments". Y axis is percent of studies where interval covers average of effect sizes. X axis is sample size of simulated study. A concave, downward-sloping line chart showing how the typical treatment effect capture rate declines as sample size increases—from above 90% at small samples to about 52% at 3,000 observations. The curve is steepest at smaller sample sizes and flattens as it grows, illustrating that increasing sample size in single-topic experiments reduces coverage of the typical effect, but at a decreasing rate.

Summary

Overall, I agree that single estimates, or studies, might provide a bad prediction of new estimates, with slightly different characteristics. Does meta-analysis, averaging across studies, provide a better prediction? I think in some cases it does, but you have to be very careful. Others are sceptical that meta-analysis should even be attempted except under very strict circumstances. I think that view can be relaxed somewhat, and hope to explain what I mean in later posts.

You May Also Enjoy